CLOSE
The small-gain theorem is a widely-used tool in the field of control theory that provides a sufficient condition for finite-gain L stability of the feedback connection. In other words, it establishes criteria to ensure that the system remains stable even when subjected to external disturbances or changes in its parameters. This theorem is particularly useful when dealing with nonlinear systems, which are known for their complex behavior and unpredictable responses.
By applying this principle, engineers and scientists can design more robust and reliable control strategies that take into account all possible scenarios and uncertainties. Moreover, the small-gain theorem enables them to optimize performance without sacrificing stability or safety, thus achieving an optimal balance between efficiency and risk mitigation. Overall, this concept has revolutionized the way we approach control problems in various domains such as aerospace engineering, robotics, electronics, and many others.
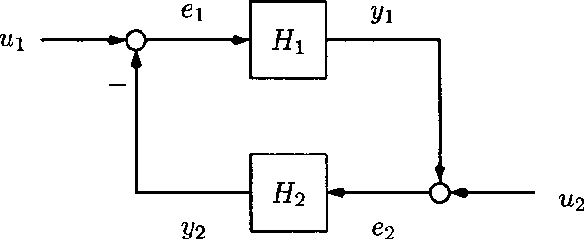
The Small-Gain Theorem is a powerful tool used to analyze the stability of nonlinear systems. When it comes to analyzing complex, interconnected systems, traditional linear techniques often fall short in providing accurate results. However, with the advantages of Small-Gain Theorem in Nonlinear Systems, engineers and researchers can now use this technique to determine whether a system will remain stable or not under different conditions.
One major advantage of using this theorem is that it allows for the analysis of an entire network rather than just individual components alone. This means that complex interconnections between different subsystems can be taken into account during modeling and simulation.
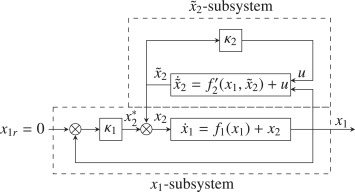
Additionally, unlike other non-linear analysis techniques, the Small-Gain Theorem provides clear guidelines on how to choose gains and feedback parameters which ensures greater accuracy when predicting system behavior over time. Overall, by harnessing the power of this theorem- experts are empowered with tools necessary for solving real-world problems in fields ranging from aerospace engineering to robotics and beyond!